UNIDAD I. CONCEPTOS BASICOS
Es una rama de las matemáticas que tiene como objetivo la resolución de problemas geométricos utilizando métodos algebraicos.
Dentro de esta rama hay conceptos como:
*Recta
*Segmento
*Longitud
*Distancia
*Coordenadas
*Pendiente
*Punto medio, etc.
Es utilizada, por ejemplo en:
-Investigación científica
-Gestion de recursos
-Arqueología
-Cartografia
-Sociología
-Geografía
-Marketing
PLANO CARTESIANO
-Creado por Rene Descartes (Turena, La Haye, 31 de marzo 1596-Estocolmo, 11 de febrero de 1650)
-En el plano Cartesiano encontramos el Origen que es el punto medio entre las Ordenadas que se encuentran en el eje de las "y" verticalmente y las Abscisas en el eje de las "x" horizontalmente
DISTANCIA ENTRE LOS PUNTOS
Para encontrar la distancia entre los puntos de utiliza la formula:
d= √(x2-x1)2+(y2-y1)2
*Raiz cuadrada del cuadrado de la diferencia de las abscisas mas el cuadrado de la diferencia de las ordenadas
PUNTO MEDIO
El punto medio es el que divide exactamente a dicho segmento en dos partes iguales.
En geometría plana lo podemos hacer utilizando una regla o compas, pero en geometría analítica cambia la situación aquí utilizamos las siguientes formulas:
Xpm= X1+X2/ 2
Ypm=Y1+Y2/2

PENDIENTE DE UNA RECTA
La pendiente de una recta es considerada como la inclinación que presenta esta con respecto a un plano horizontal, ejemplo, un avión al despegar se desliza a una velocidad sobre una pista que es nuestro plano horizontal al obtener cierta velocidad y distancia se eleva.
La pendiente de un segmento de recta se puede obtener mediante el cociente de la diferencia de las ordenadas entre la diferencia de las abscisas:
Mab= Y2-Y1/X2-Y1
UNIDAD II. LA RECTA
La recta se puede definir como una sucesión de puntos indefinidos que no tienen una dirección fija.
Las rectas pueden tener cualquier posición y sus ángulos de inclinación puedes ser de 0 a 360°
TABULACION DE UNA RECTA
Una recta se puede representar mediante la construcción de una tabulación y transferirla a un plano cartesiano. Siempre el lugar geométrico de una recta será una línea
f (x) =x
y = x
EJEMPLO:
FORMAS DE LA ECUACION EN LA RECTA
1.- FORMA GENERAL
La ecuación general de una recta es una expresión de la forma Ax+By+C=0. En donde Ax representa forma la forma lineal en “X”. By representa la forma lineal en “y” y por último la c representa la forma independiente.
2.- FORMA PUNTO PENDIENTE
Para aplicar esta forma requerimos las coordenadas de un punto y la pendiente de la recta en. En caso de que no tengamos la pendiente se hace necesario tener 2 coordenadas que formen una recta.
En el caso de no tener la pendiente pero teniendo las coordenadas se utiliza la igualdad:
En el caso de no tener la pendiente pero teniendo las coordenadas se utiliza la igualdad:
La igualdad para encontrar la forma de la recta punto-pendiente es:
Que se relaciona directamente con la forma general, ya que cuando aplicamos la igualdad anterior tenemos como resultado una ecuación lineal de primer grado.
Una vez obtenido la ecuación se procede a obtener la gráfica. Se procede a igualar a 0 el término en “y” (este procedimiento se hace solo cuando te dan la coordenada de un solo punto)
3.- FORMA PENDIENTE Y ORDENADA EN EL ORIGEN
Consideramos como (Forma pendiente ordenada al origen) aquel método que involucra la determinación de la (ecuación de una recta) en un estado donde la pendiente de la misma produce el hecho de que cuando se evalua en el punto (0,y) nos arroge como resultante la ordenada (El valor “Y”) correspondiente a justamente donde se produce una intersección con el eje “Y” en un (Sistema de coordenadas bidimensional).
Para este tipo de ecuación siempre se da la forma general (Ax+By+C). Para graficar esta forma se tiene que despejar el elemento en “x” y posteriormente el elemento en “y”
4.- FORMA REDUCIDA
*Simplemente consiste en igual a 0
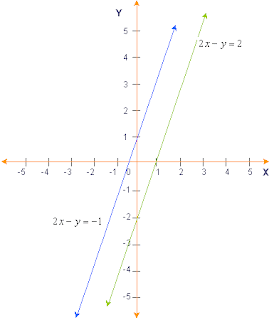
PARALELISMO Y PERPENDICULARIDAD
Dos rectas son paralelas cuando can a mantener la misma distancia de separación.
*Para el matemático y filosofo Euclides las rectas paralelas nunca se cortan entre si, otros estudios avanzados de geometría han cuestionado lo que afirmaba. Para la geometría analítica dos rectas que son paralelas van a tener la MISMA PENDIENTE.
m1=m2
En este tipo de problema, solo encontramos la ecuación de la recta donde se proporcionan dos puntos de la misma. Al proporcionar dos untos de la recta me están dando un segmento de la misma.
La siguiente parte de un problema así consiste en utilizar la misma pendiente con las coordenadas del punto x.
NOTA: Cuando las rectas son paralelas las pendientes van a ser iguales y el termino líneas en "x" y en "y" coinciden. Los términos independientes son diferentes.
Podemos afirmar que dos rectas perpendiculares son cuando dormán exactamente 90° al intersectarse o cortarse.
Las pendientes de las rectas perpendiculares son inversas y de signo contrario.
Para encontrar la recta perpendicular de una recta, se obtiene primero la pendiente y posteriormente se debe obtener la formula general. Por ultimo se iguala a 0 para obtener las otras dos coordenadas.
UNIDAD III. LA CIRCUNFERENCIA
Es una línea cerrada, cuya característica principal es que todos los putos equidistan de otro punto fijo llamado centro.
Una circunferencia esta determinada por el centro y el radio de la misma.
LINEAS Y SEGMENTOS DE LA CIRCUNFERENCIA
* Cuerda: segmento que une dos puntos cualesquiera de la circunferencia
*Diámetro: cuerda que pasa que pasa por el centro
*Arco: Cada una de las partes en que una cuerda divide a la circunferencia
*Semicircunferencia: Arcos iguales que abarca un diámetro.
ECUACION DE LA CIRCUNFERENCIA CON CENTRO EN EL ORIGEN
En este caso la abscisa y la ordenada del centro de la circunferencia se encuentran en el origen, solamente debemos conocer el valor del radio.
Si nos proporcionan el centro (el origen) y dos puntos que van a ser el diámetro.
En este caso se pueden hacer 2 situaciones:
1) Obtener el punto que su resultado debe ser (0,0)
2) De otra forma se obtiene el valor del radio como en el caso anterior.
Para encontrar el lugar geométrico a partir de la ecuación. Existen 3 posibilidades:
A) La circunferencia sea real
B) La circunferencia sea imaginaria
C) Que solo sea un punto
ECUACION DE LA CIRCUNFERENCIA CON CENTRO FUERA DEL ORIGEN
En este caso vamos a resolver nuestros problemas utilizando la siguiente formula:
En donde las literales "h" y "k" son las coordenadas del centro de la circunferencia.
La forma general para encontrar la ecuación de un circunferencia es:
En este tipo de problemas nos van a proporcionar el centro, h, k y las coordenadas de un punto por donde pasa la circunferencia. En este caso vamos a encontrar la distancia entre los puntos, con la siguiente formula:
UNIDAD IV. LA PARABOLA
Es una curva abierta y plana que se define como el lugar geométrico de laos puntos del plano que equidistan de un punto determinado llamado foco.